A Walk is defined as a sequence of steps of connected graph vertices and graph edges. Functional Walks are generated by using a main function f(n) and an additional step function g(n): (1) We are at some point w(n) = (x(n),y(n)). For n = 0 we define w(0) = (0,0). (2) We divide the 360 degrees or 2π in N equal directions. (3) We calculate the direction for the next step by



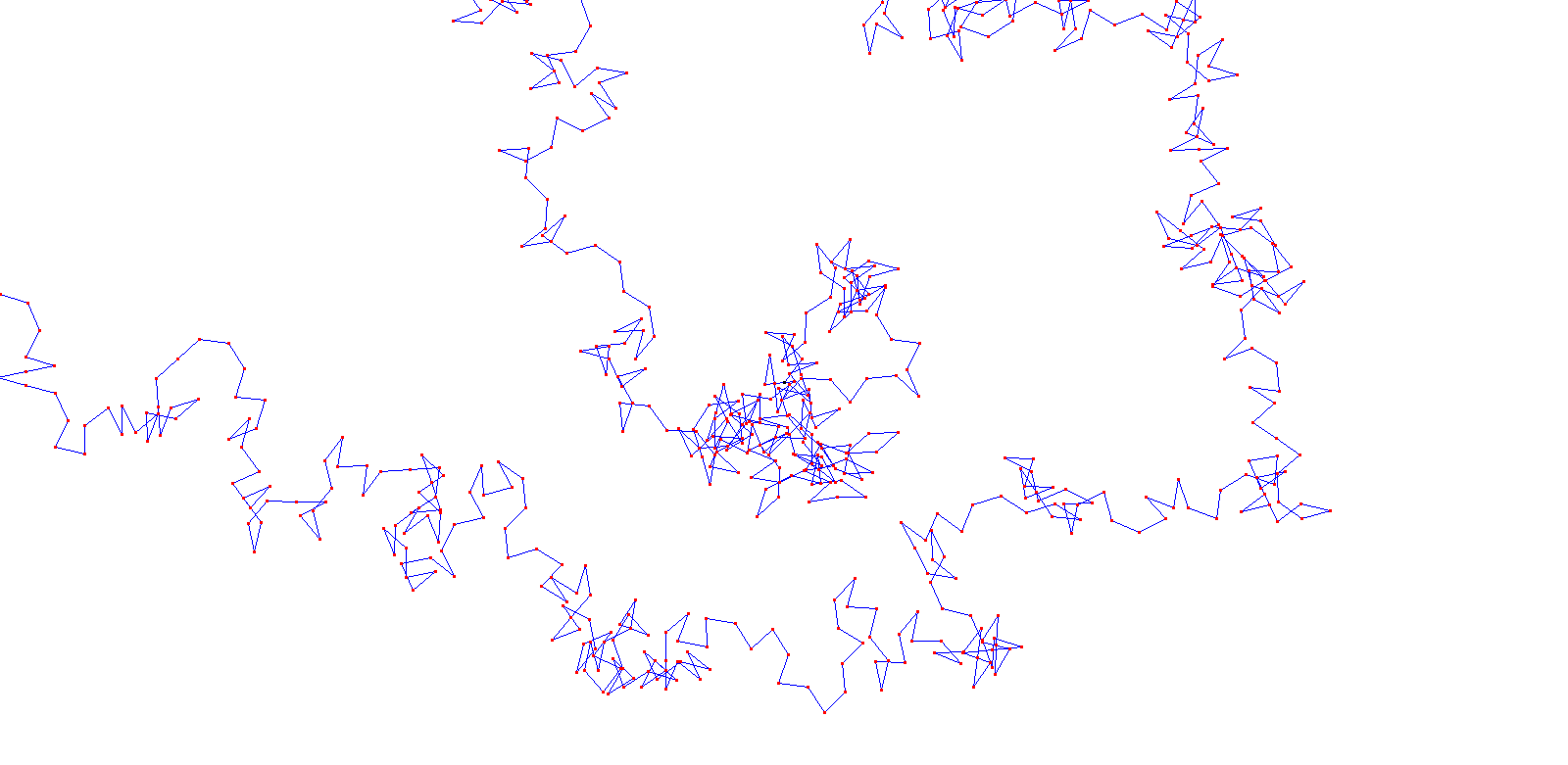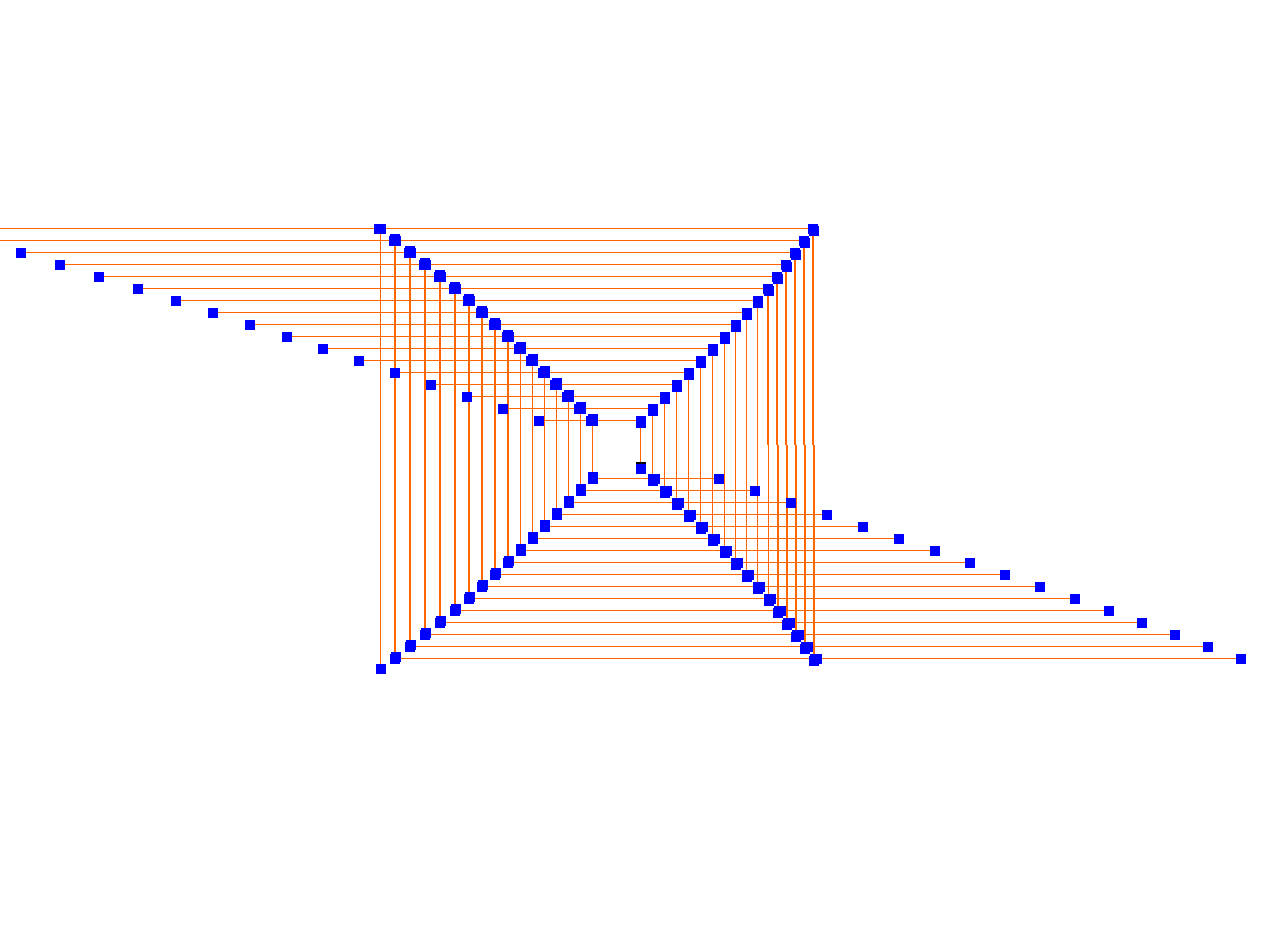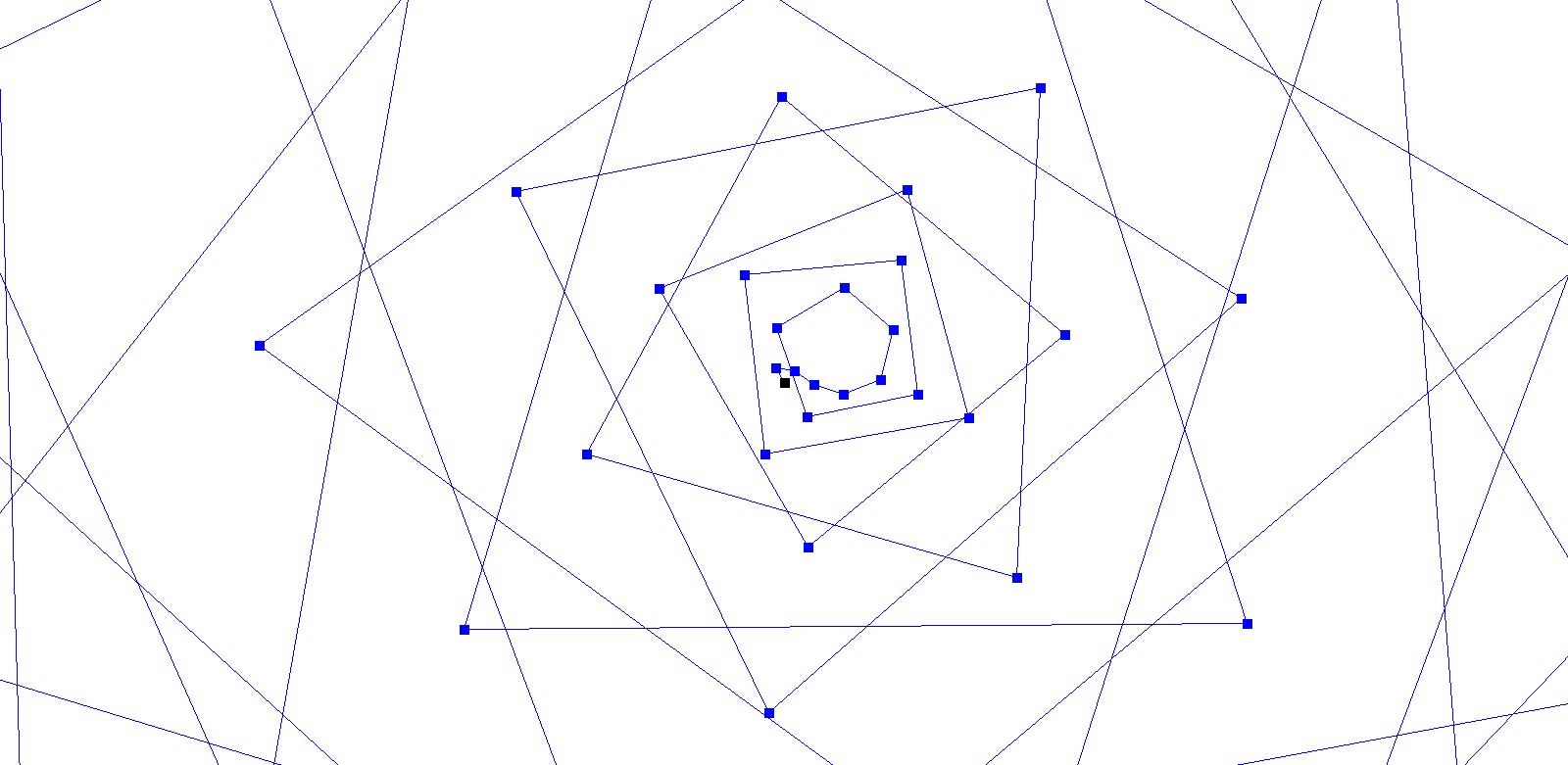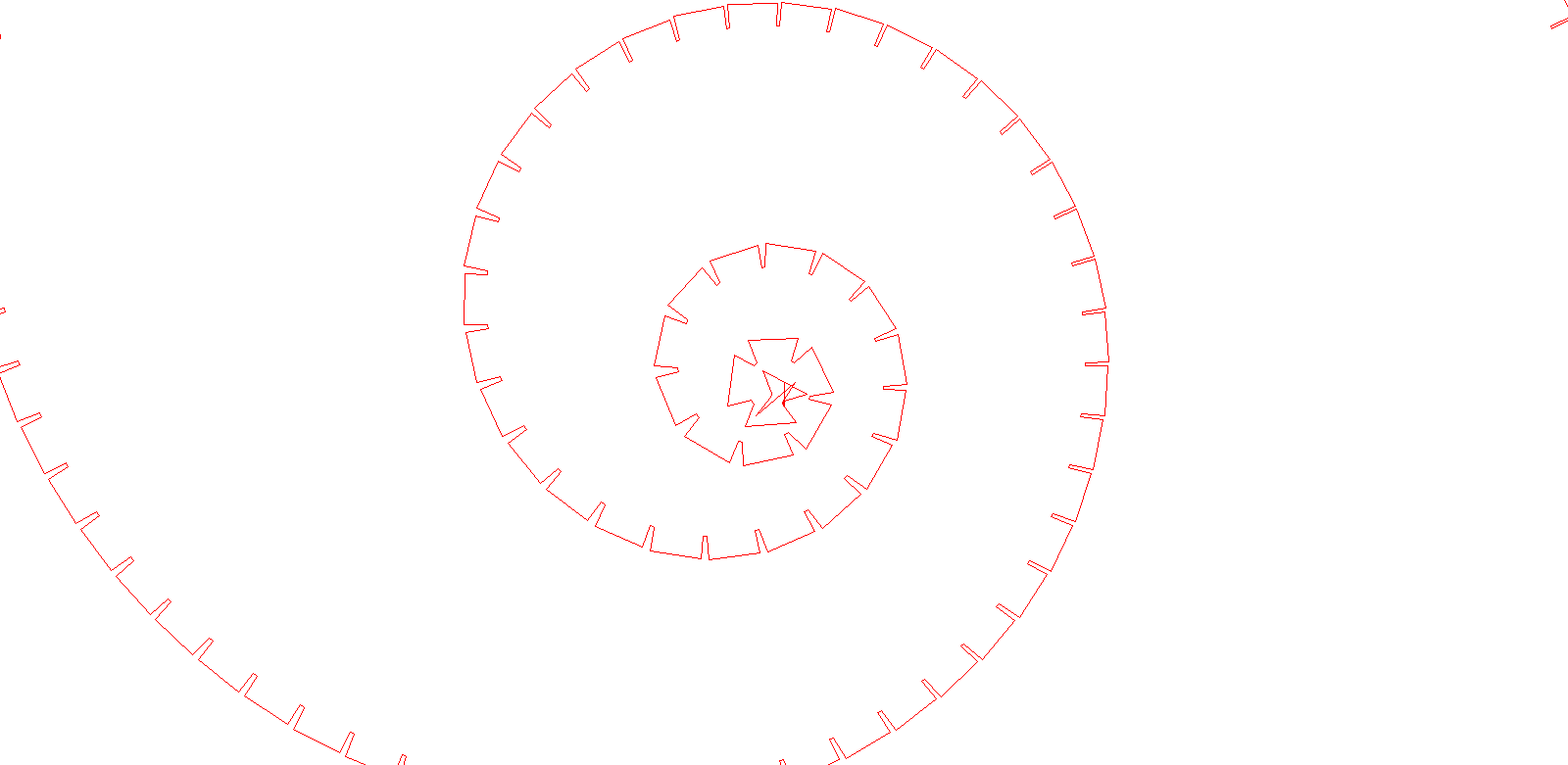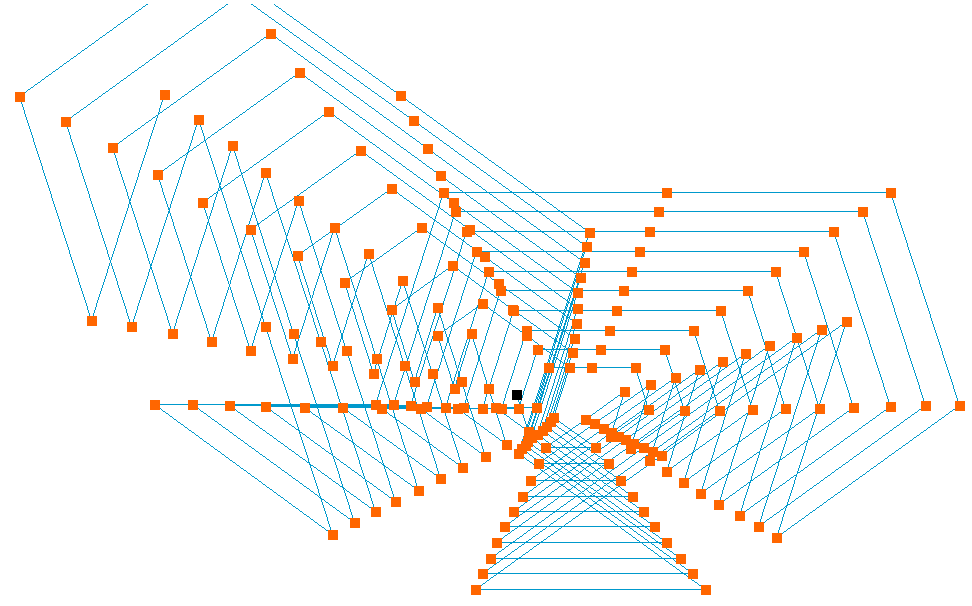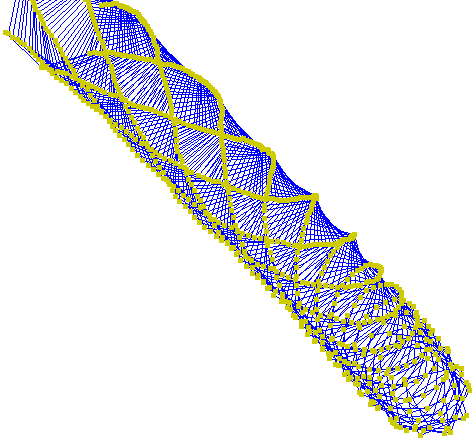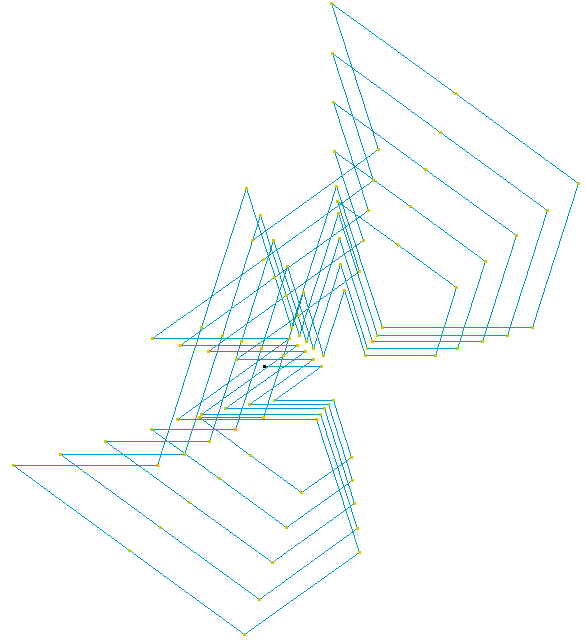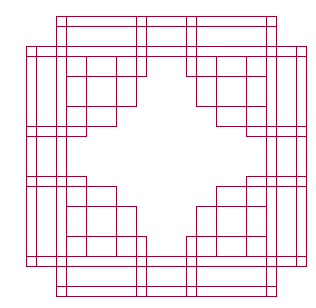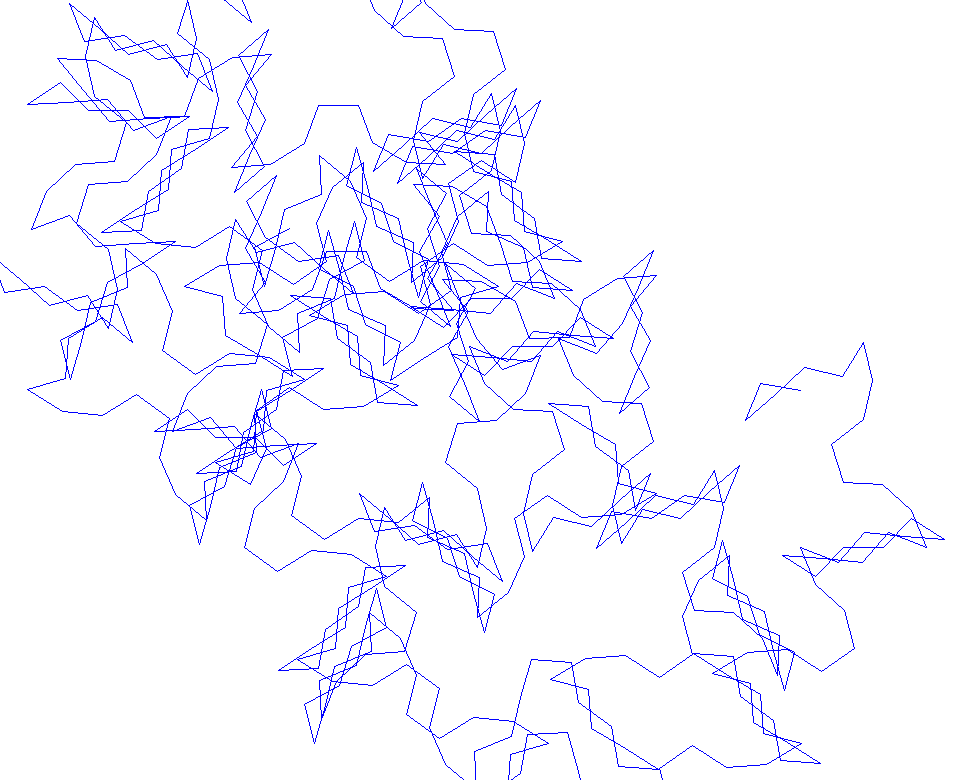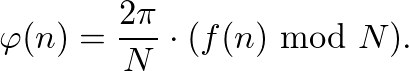
(4) We move g(n) units in this direction and repeat the process.
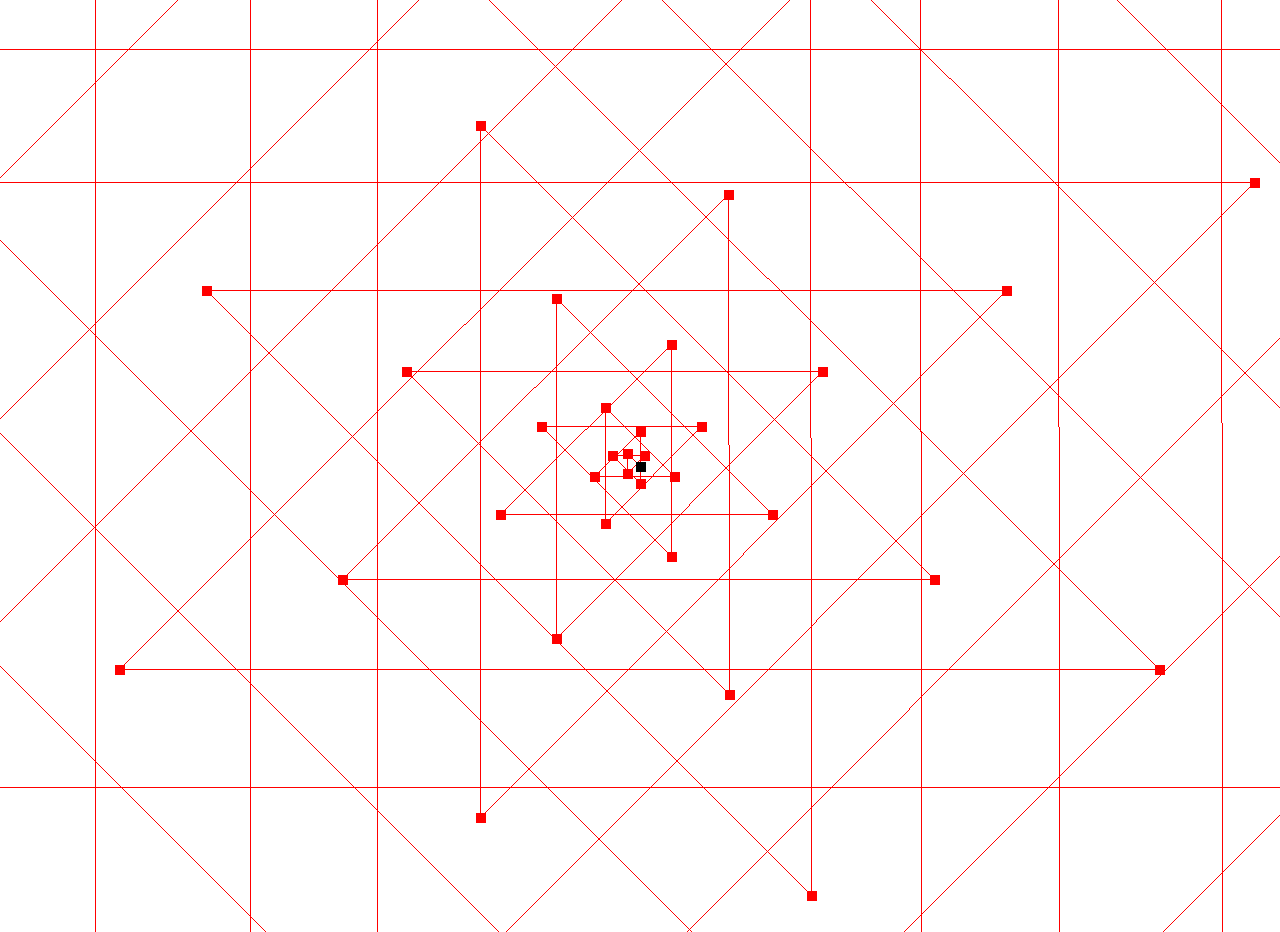
This process can be summarized through the recursion



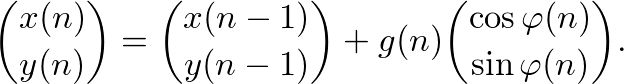
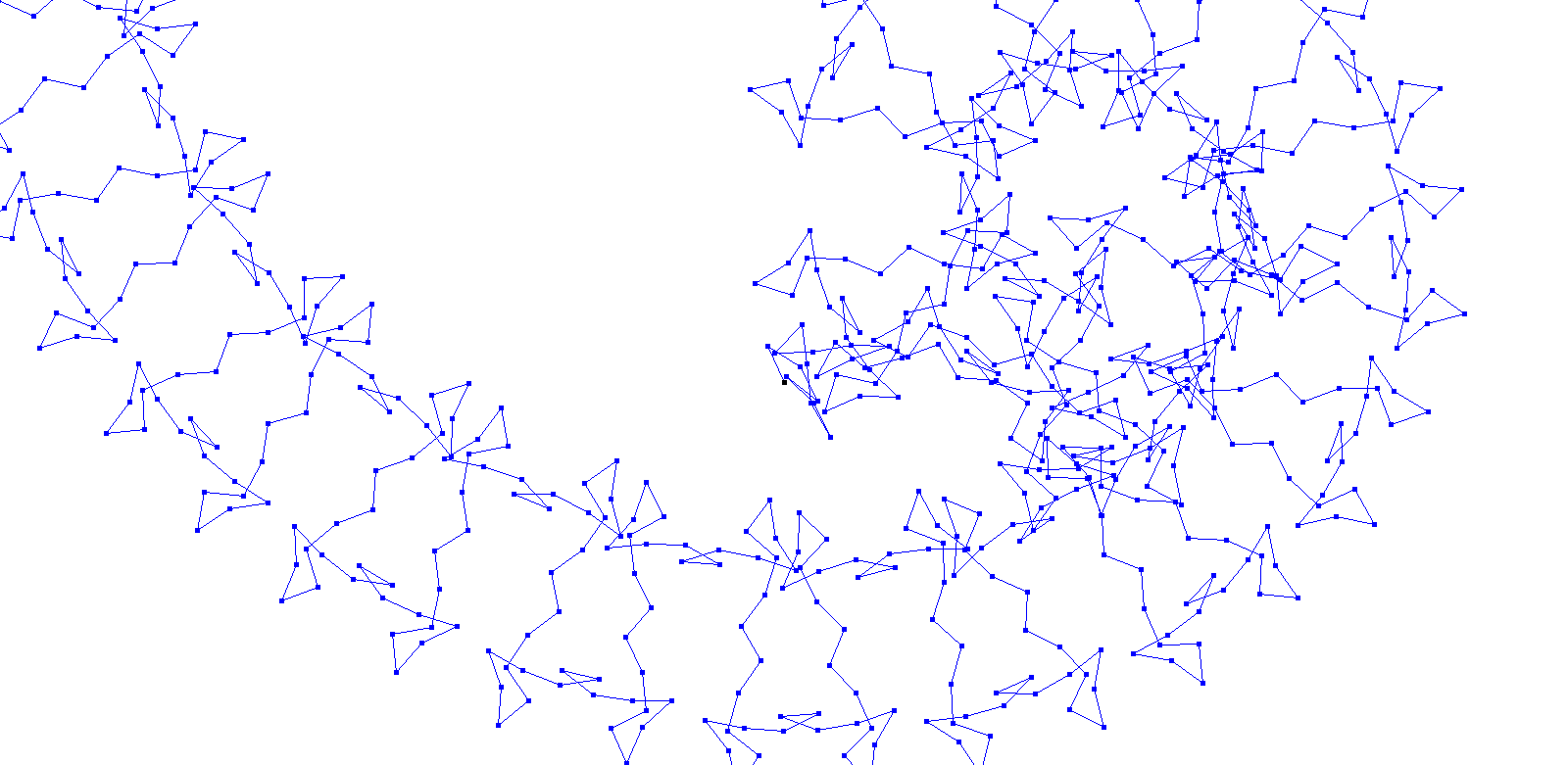
The walk is generated by adding steps, which may be represented as vectors.
The recursion yields for the position (x,y) at a given moment n



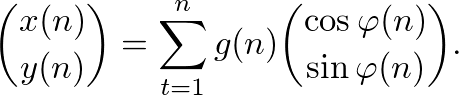
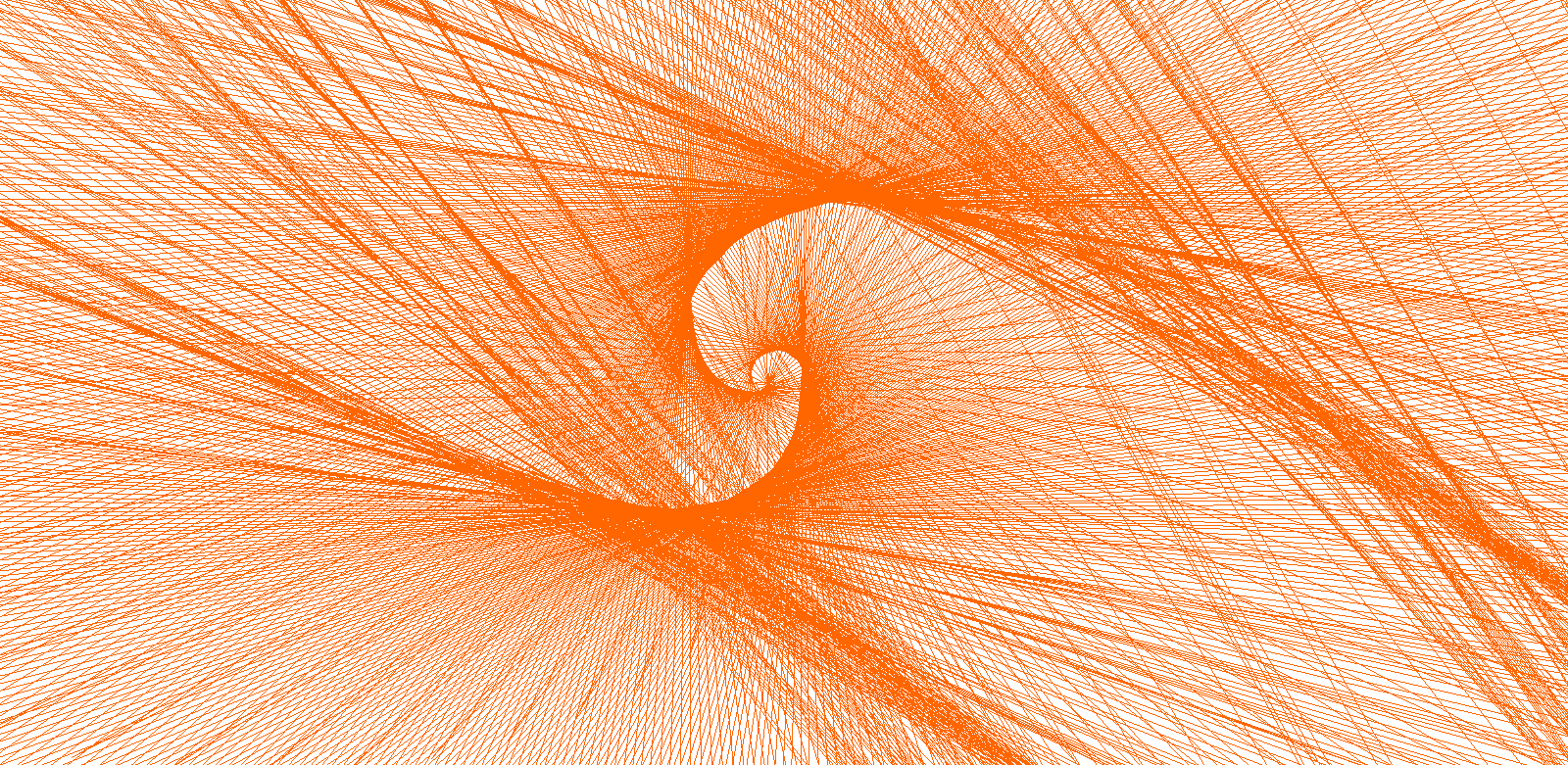
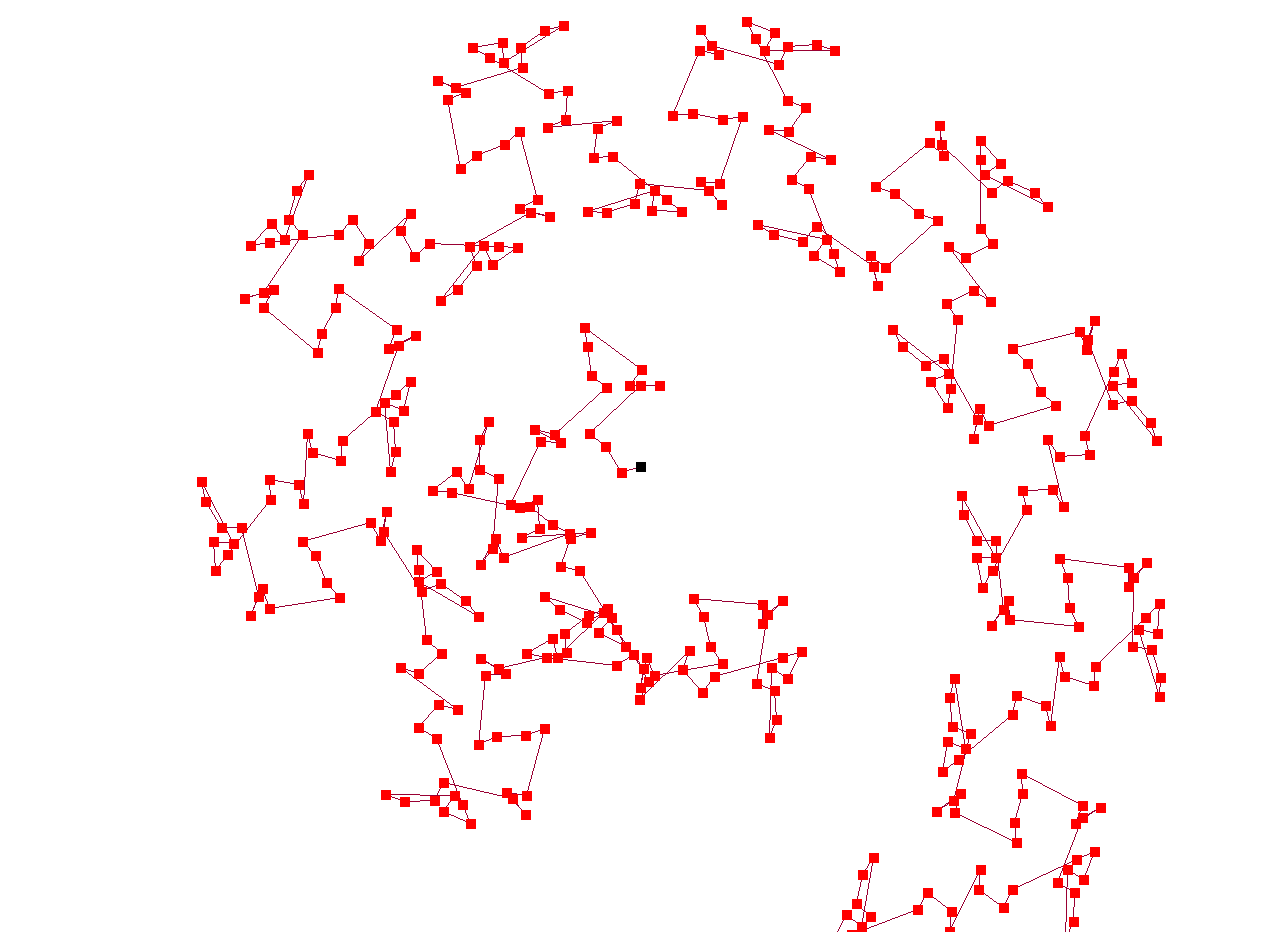
The hole walk is therefore given by W(f,g,N). Fascinating patterns emerge very quickly, e.g. by applying f(n) = n. But also a variety of challenges and research opportunities arises when explaining patterns, predicting walks, describing walks as curves or investigating further properties.